Smith Predictor
-
I have a process that I am controlling using a PLC with a PI controller that is very very slow, process takes around two hours to get up to setpoint and most often over shoots excessively.
I am looking at using the Smith Predictor as a way to control my process (example project 0303-29). I see where I can insert my SP but dont understand where I would insert my PV, would it be the CNR_INP_DIST?
Can this Smith Predictor example be used in a real world application? Of course with some minor changes!
Also I have a license GY8G-H7MH-2U5A-8IFC-9X7U-9XT4-P8IK-LMXU and am trying to use the PIDMA but am getting a error that says I dont have the capability to use that FB. -
Nevermind about the PIDMA, looks like I need to upgrade if I want that.
-
See if I am understanding this correctly.
The 'smith predictor - process model' is my software process. I've updated the gain, Tc, and DeadTime with my known real world process. If I wanted to use this smith predictor example for real world applications I would remove the 'smith predictor - process model' with my real PV signal? -
Dear Ryan,
the task "Smith predictor - process model" is a model of the controlled process/plant. In a real-world application, you'll exclude the whole task from your project. In the control task, you'll replace the greenpvInport andmvOutport with I/O signals.The Smith_Predictor subsystem in the control task is where you should change the gain, time constant and dead time to match your controlled process/plant. Plus I guess you'll want to replace the MDL blocks with FOPDT blocks.
Can you share the gain, time constant and dead time of your process? I understand the process response is quite slow, but it's the ratio between dead time and time constant which is the most important for the decision whether to use Smith predictor or not. There are many processes which are easy to control even with a simple PI/PID controller, no matter how sluggish their response is.
Best regards
Jaroslav -
Good morning Jaroslav,
My process ranges:
Gain .028 - .093
TimeConstant 25min - 90min
DeadTime 7min - 12min -
Currently I'm using the Smith example, I've removed the SOPDT in the Smith predictor with FOPDT as you suggested.
In the top FOPDT I have:
Ko .093
del 720
tau 5400In the bottom FOPDT I have:
Ko .028
del 420
tau 1500In the process model I have:
Ko .059
del 540
tau 3600
tau2 4200In the PIDMA I have:
picture attatched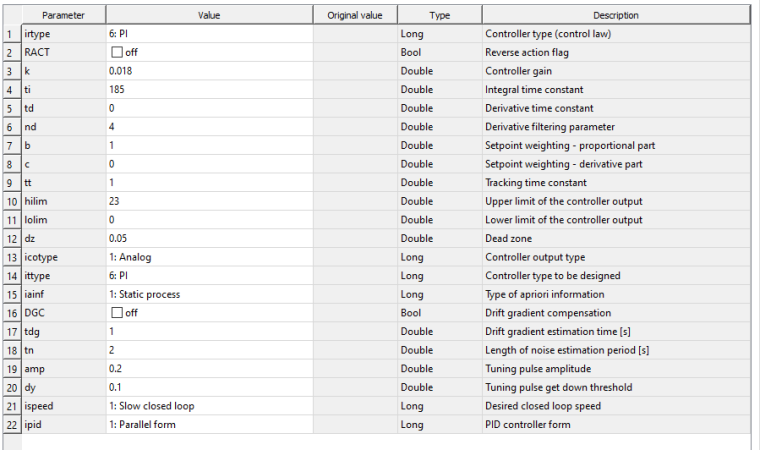
I am constantly overshooting this simulation, any ideas?
-
Dear Ryan,
thanks for the parameters. If the controlled plant is defined by
K=0.059
del=540
tau1=3600
tau2=4200
then there is no need to use Smith predictor. A simple PI (k=16.859, ti=5866.1) or PID controller will work fine.However, if you insist on using the Smith predictor, then the blocks inside the Smith_predictor subsystem should be as close to the controlled plant as possible. Because tau1 and tau2 are close to each other, you should use MDL function block as in the original example. And for sure, the only difference between the upper and lower block in the Smith_predictor subsystem should be the time delay. The gain and time constants must be the same.
The parameters which you provided can hardly lead to satisfactory closed loop performance.
Best regards
Jaroslav -
This post is deleted! -
What technique did you use to derive the k=16.859, ti=5866.1?
-
@ryanastiefes Dear Ryan,
I have used PID Control Laboratory at www.pidlab.com.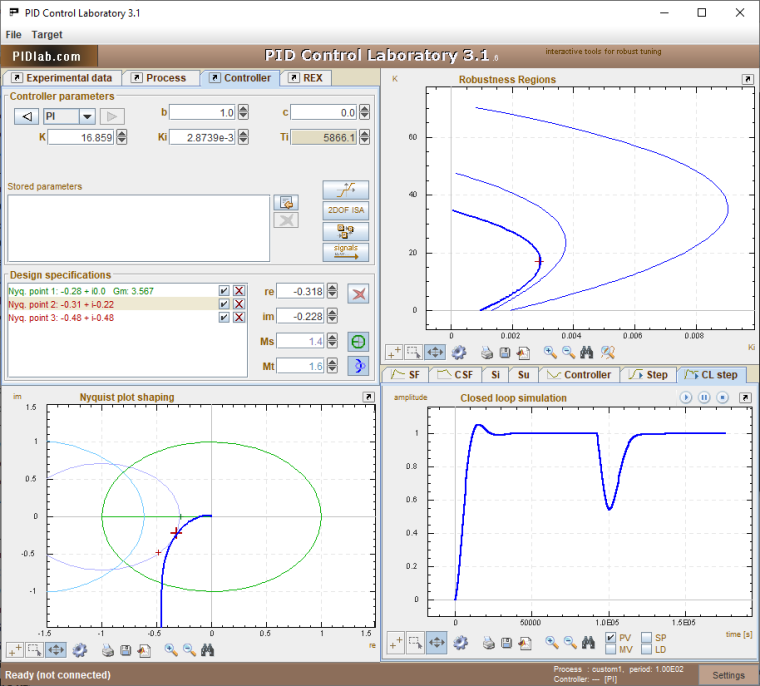
Hope this helps.
Best regards
Jaroslav