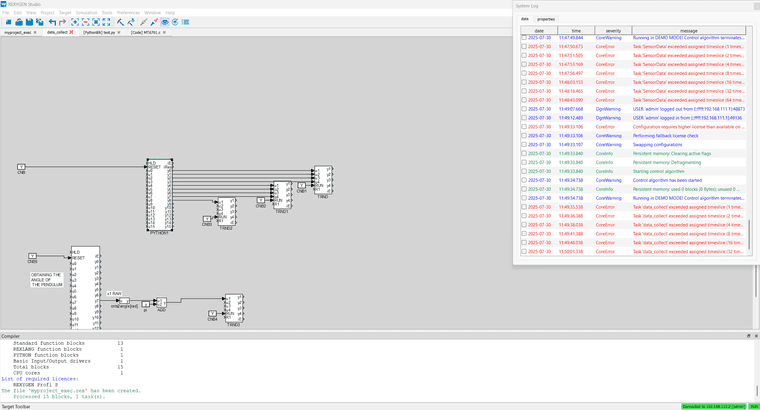
I am not quite sure what this error means or how to fix it if any knows
Posts made by har
-
Core errorposted in General
-
Bluetooth sensor with rexygenposted in Communication (RS232
Hi I am trying to find a way to get my bluetooth sensor(Witmotion WT9011DCL 9-axis BLE Magnetometer Gyroscope) to communiate with rerxygen so I can stream the data into rexygen. I have been able to connect the sensor with my raspberry Pi 4 monacrohat. I then tried to stream the data into rexygen but have been unable to do so. I have attached the my program below.
# coding:UTF-8 import asyncio import bleak from PyRexExt import REX class DeviceModel: def __init__(self, deviceName, BLEDevice, callback_method): self.deviceName = deviceName self.BLEDevice = BLEDevice self.client = None self.writer_characteristic = None self.isOpen = False self.callback_method = callback_method self.TempBytes = [] async def openDevice(self): try: async with bleak.BleakClient(self.BLEDevice, timeout=15) as client: self.client = client self.isOpen = True print("Device connected.") REX.y9.v = 1 # Connected target_service_uuid = "0000ffe5-0000-1000-8000-00805f9a34fb" target_characteristic_uuid_read = "0000ffe4-0000-1000-8000-00805f9a34fb" target_characteristic_uuid_write = "0000ffe9-0000-1000-8000-00805f9a34fb" notify_characteristic = None for service in client.services: if service.uuid == target_service_uuid: for char in service.characteristics: if char.uuid == target_characteristic_uuid_read: notify_characteristic = char if char.uuid == target_characteristic_uuid_write: self.writer_characteristic = char if self.writer_characteristic: await self.sendData([0xFF, 0xAA, 0x24, 0x01, 0x00]) # 6-axis mode await self.sendData([0xFF, 0xAA, 0x03, 0x09, 0x00]) # 100 Hz if notify_characteristic: await client.start_notify(notify_characteristic.uuid, self.onDataReceived) while self.isOpen: await asyncio.sleep(1) await client.stop_notify(notify_characteristic.uuid) else: print("Notify characteristic not found.") REX.y9.v = 2 # Failed except Exception as e: print("BLE connection failed:", e) REX.y9.v = 2 # Failed def onDataReceived(self, sender, data): bytes_list = list(data) self.TempBytes.extend(bytes_list) if len(self.TempBytes) >= 20: if self.TempBytes[0] == 0x55 and self.TempBytes[1] == 0x61: self.processData(self.TempBytes[:20]) self.TempBytes = [] def processData(self, Bytes): def get_val(low, high, scale): raw = (high << 8) | low val = raw - 65536 if raw >= 32768 else raw return round(val / 32768 * scale, 3) acc_x = get_val(Bytes[2], Bytes[3], 16) acc_y = get_val(Bytes[4], Bytes[5], 16) acc_z = get_val(Bytes[6], Bytes[7], 16) gyro_x = get_val(Bytes[8], Bytes[9], 2000) gyro_y = get_val(Bytes[10], Bytes[11], 2000) gyro_z = get_val(Bytes[12], Bytes[13], 2000) ang_x = get_val(Bytes[14], Bytes[15], 180) ang_y = get_val(Bytes[16], Bytes[17], 180) ang_z = get_val(Bytes[18], Bytes[19], 180) # Send to REXYGEN outputs REX.y0.v = acc_x REX.y1.v = acc_y REX.y2.v = acc_z REX.y3.v = gyro_x REX.y4.v = gyro_y REX.y5.v = gyro_z REX.y6.v = ang_x REX.y7.v = ang_y REX.y8.v = ang_z print("Data:", acc_x, acc_y, acc_z, gyro_x, gyro_y, gyro_z, ang_x, ang_y, ang_z) async def sendData(self, data): try: if self.client and self.writer_characteristic: await self.client.write_gatt_char(self.writer_characteristic.uuid, bytes(data)) except Exception as e: print("Write failed:", e) class BLEScanner: def __init__(self, target_mac="CC:0E:4F:3B:A4:3B"): self.target_mac = target_mac self.BLEDevice = None self.device_model = None async def scan_and_connect(self): try: print("Scanning for BLE devices...") devices = await bleak.BleakScanner.discover(timeout=10.0) for d in devices: if d.address == self.target_mac: self.BLEDevice = d break if not self.BLEDevice: print("Target device not found.") REX.y9.v = 2 return self.device_model = DeviceModel("MyBLE", self.BLEDevice, None) await self.device_model.openDevice() except Exception as e: print("Scan or connect error:", e) REX.y9.v = 2 def run_ble_task(): loop = asyncio.new_event_loop() asyncio.set_event_loop(loop) scanner = BLEScanner() loop.run_until_complete(scanner.scan_and_connect()) loop.close() # Main entry point for REXYGEN if __name__ == "__main__": print("Starting REXYGEN BLE program") REX.y9.v = 2 # Default = failed run_ble_task() -
Bluetooth sensorposted in General
Hi I am trying to connect my bluetooth sensor(Witmotion WT9011DCL 9-axis BLE Magnetometer Gyroscope) to rexygen via bluetooth so I can stream the data from the sensor into rexygen. I am not sure how to get started on this.
-
Connection Problemposted in Communication (RS232
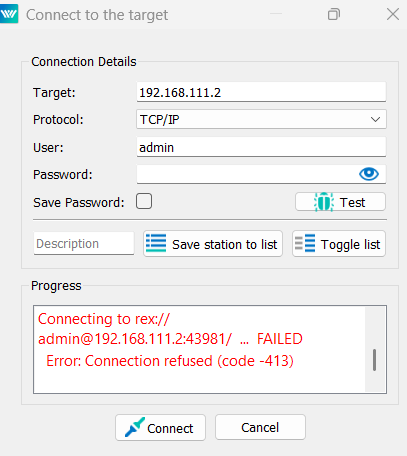
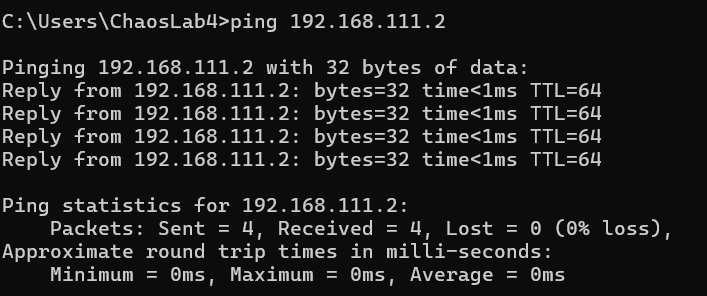
I am unable to conneect to the rexygen to my Raspberry Pi.
-
RE: Complier issueposted in REXYGEN Studio
@cechurat Hi Thomas when I hover my mouse over the error I get this message.

I am not quite sure what it means or how to fix it
-
RE: Complier issueposted in REXYGEN Studio
@cechurat

I think the problem might be in the python block.import numpy as np
import time
from numpy import sin,cos,pi
from scipy.integrate import solve_ivp, solve_bvp, quad, odeint
from scipy.linalg import solve_continuous_are
from scipy.interpolate import interp1d
#import matplotlib.pyplot as plt
from PyRexExt import REXdef init():
global ω,ζ,π,τ,τ1,τpred,xmax,umax,θinti,θdotinit,xinit,xdotinit,xstate_init,θend1,θend2,θdotend,xend,xdotend,xstate_end1,xstate_end2,Q,R,ts,dt,ts1,bvpfcn,bcfcn,ff,uff0,uff,runningCost,A,B,mRiccati,Sall,Ball,Kall,fpred,us,j
global xstate_end,FFsol,X,uff,vs,Kvec,Xlast,Klast############################################ Define parameters ω = REX.u1.v ζ = REX.u2.v; # pendulum friction (scaled: 1 = critical damping) π = pi; # π = 3.14159... τ = 2*π # swingup time = 1 period, in scaled units τpred = 1 # allow for calculation time, in scaled units τ1 = 2*τ # for sim: swingup + balance time xmax = 2; # track limits at ±xmax umax = 5; # clip u for simulation test ONLY (not design) θinit = 0; # initial angle of pendulum θdotinit = 0.0; # initial angular velocity of pendulum xinit = 0.0; # initial position of cart xdotinit = 0.0; # initial velocity of cart xstate_init = np.array([θinit,θdotinit,xinit,xdotinit]) # eventually, from expt. θend1 = π # CCW swingup, assume θinit ∊ (-π,π) θend2 = -π # CW swingup θdotend = 0.0; # final angular velocity of pendulum xend = 0.0 * xmax; # final cart position xdotend = 0.0; # final cart velocity xstate_end1 = np.array([θend1,θdotend,xend,xdotend]) # modify for swing down, transport, ... xstate_end2 = np.array([θend2,θdotend,xend,xdotend]) # modify for swing down, transport, ... Q = np.diag([1,10,1,1]) # weighting for states for LQR R = np.array([10]) # weighting for input for LQR ts = np.arange(0, τ, 0.01*ω) # swing up in τ dt = 0.01*ω ts1 = np.arange(0, τ1, 0.01*ω) # swing up in τ, balance for another τ ############################################# Define functions def bvpfcn(t, X): # solve coupled state-adjoint system θ, θdot, x, xdot, λθ, λθdot, λx, λxdot = X dX = np.zeros((8, X.shape[1])) # array dimension is 8 * nx sinθ = sin(θ); cosθ = cos(θ) u = -λxdot + λθdot*cosθ dX[0] = θdot dX[1] = -sinθ - u*cosθ dX[2] = xdot dX[3] = u dX[4] = λθdot * (cosθ - u*sinθ) dX[5] = - λθ # dX[6] = -x**3 / xmax**4 # or: from running cost term (x/xmax)**4 dX[6] = 0 # running cost independent of x dX[7] = -λx return dX # Return derivatives (array) def bcfcn(x0, xτ): # boundary conditions for 4d-state at t = 0, τ dx0 = x0[0:4] - xstate_init # boundary condition for 4d state at t=0 dxτ = xτ[0:4] - xstate_end # bc at t=τ return np.hstack((dx0,dxτ)) # 8-dim vector for solve_bvp def ff(x0,xτ,τ): # ff state x0 → xτ in τ θinit,_,xinit,_ = x0 θend, _,xend, _ = xτ nt = 21 # number of time points, to start tvec = np.linspace(0, τ, nt) xλguess = np.zeros((8, nt)) # initial guesses for state trajectories xλguess[0, :] = np.linspace(θinit, θend, num=nt) # θ linear, θinit → θend xλguess[2, :] = np.linspace(xinit, xend, num=nt) # x linear, xinit → xend FFsol = solve_bvp(bvpfcn, bcfcn, tvec, xλguess, tol=0.1) # solve boundary-value problem return FFsol.sol def uff0(t): # feedforward acceleration (cannot evaluate on arrays) θ,_,_,_,_,λθdot,_,λxdot = FFsol(t) # evaluate interp funcs at time=t uff0 = -λxdot + λθdot*cos(θ) if t<τ else 0 return uff0 uff = np.vectorize(uff0) # define vectorized version (can call with array) def runningCost(t): # to calc cost of the feedforward command return 0.5*uff0(t)**2 def A(t): # dynamical matrix (local linear, nominal) θ = FFsol(t)[0] # FFsol from FF function Amat = np.zeros((4,4)) # 4 is from xstate.shape[0] Amat[0,1] = 1 Amat[1,0] = -cos(θ) + uff(t)*sin(θ) Amat[1,1] = 0 Amat[2,3] = 1 return Amat # evaluated at time t def B(t): # input vector (local linear, nominal) θ = FFsol(t)[0] # FFsol from FF function Bmat = np.zeros((4,1)) # 4 is from xstate.shape[0] Bmat[1] = -cos(θ) Bmat[3] = 1 return Bmat def mRiccati(t,S): # derivatives for matrix Riccati (vector form) Smat = S.reshape((4,4)) # convert 16 vector to 4x4 matrix A0 = A(t) # current dynamical matrix B0 = B(t) # current input vector dSmat = - A0.T @ Smat - Smat @ A0 - Q + Smat @ (B0 @ B0.T) @ Smat / R[0] dS = dSmat.reshape((16)) # convert 4x4 matrix to 16 vector return dS def Sall(Send,τ,tvec): # S matrix evaluated at times tvec Send1 = Send.reshape((16)) t_span = (τ, 0) # solve backwards in time, from τ → 0 Ssol1 = solve_ivp(mRiccati, t_span, Send1, dense_output=True).sol return Ssol1(tvec).reshape(4,4,tvec.size) # evaluate on tvec def Ball(FFsol,tvec): # input matrix (local linear, nominal) θ = FFsol(tvec)[0] nt = tvec.size Bmat = np.zeros((4,nt)) # 4 is from xstate.shape[0] Bmat[1] = -cos(θ) Bmat[3] = np.ones((nt)) return Bmat def Kall(Send,FFsol,τ,tvec): # for graphing tvec1 = np.clip(tvec, 0, τ) # elements beyond ff range are clipped to limits S = Sall(Send,τ,tvec1) # 4 x 4 x nt matrix (nt copies of 4x4 matrix B = Ball(FFsol,tvec1) # 4 x nt matrix (nt copies of 4-vector) return np.einsum('ijk,jk->ik', S, B)/R[0] # sum over inner index, element-mult tvec index def fpred(t,xstate): # dynamical eqs, for constant-v input θ, θdot, _, xdot = xstate # dynamical states dX = np.zeros((4)) # 4 is from xstate.shape[0] dX[0] = θdot dX[1] = -sin(θ) - 2*ζ*θdot # sim has pendulum friction, even if ff does not dX[2] = xdot dX[3] = 0 # driving term is vtot; utot is a derived variable return dX ############################################# prediction of future state xpred = solve_ivp(fpred, (0, τpred), xstate_init, dense_output=True).sol # predict future state xstate_init = xpred(τpred) # "initial" state, as predicted τpred in future θ0 = xstate_init[0]; # extrapolated θ0 might not be ∊ (-π,π) θ1 = (θ0+π) % (2*π) - π # modulus 2π xstate_init[0] = θ1 # new angle is ∊ (-π,π) ############################################# FF calculations xstate_end = xstate_end1; θend = θend1 FFsol = ff(xstate_init,xstate_end,τ) # ff solution for 4-state and 4-adjoint, 0→τ FFsol1 = FFsol Jff1 = 0.5*np.sum(uff(ts)**2)*dt # integrated running cost = overall cost xstate_end = xstate_end2; θend = θend2 FFsol = ff(xstate_init,xstate_end,τ) # ff solution for 4-state and 4-adjoint, 0→τ FFsol2 = FFsol Jff2 = 0.5*np.sum(uff(ts)**2)*dt # integrated running cost = overall cost REX.y11.v = f"feedforward cost: θend = π, Jff1 = {Jff1:0.2f}, θend = -π, Jff2 = {Jff2:0.2f}" if (Jff1 < Jff2): FFsol = FFsol1; xstate_end = xstate_end1 else: FFsol = FFsol2; xstate_end = xstate_end2 ############################################### fb calculations Aend = A(τ) # linear dynamics A matrix at t=τ Bend = B(τ) # linear input-coupling B vector at t=τ Send = solve_continuous_are(Aend,Bend,Q,R) # static S matrix from ARE Kvec = Kall(Send,FFsol,τ,ts1) # feedback gain vectors for t in ts1 ############################################### get arrays θs,θdot,x, xdot,_,_,_,_ = FFsol(ts) X = np.array([θs,θdot,x,xdot]) θlast,θdotlast,xlast,xdotlast,_,_,_,_=FFsol(2*π) # Evaluate last values Xlast = np.array([[θlast],[θdotlast],[xlast],[xdotlast]]) X = np.hstack((X,Xlast)) # add last value Klast = Kall(Send,FFsol,τ,2*π+0.1) Kvec = np.hstack((Kvec,Klast)) vs = np.hstack((xdot,0)) j=0def main():
start_test = time.perf_counter()
global j,X,uff,vs,Kvecif not REX.u0.v and j == 0: return else: REX.y15.v = True REX.y10.v= f"len(X)={len(X[0])}" if (j >= len(X[0])): REX.y8.v = 0 return # Value for every time REX.y0.v = X[0][j] REX.y1.v = X[1][j] REX.y2.v = X[2][j] REX.y3.v = X[3][j] REX.y4.v = Kvec[0][j] REX.y5.v = Kvec[1][j] REX.y6.v = Kvec[2][j] REX.y7.v = Kvec[3][j] REX.y8.v = vs[j] j += 1 test_time = time.perf_counter() - start_test REX.y9.v = f"test time = {test_time:0.3f} s" returndef exit():
# PUT YOUR CODE HERE
return -
Complier issueposted in REXYGEN Studio
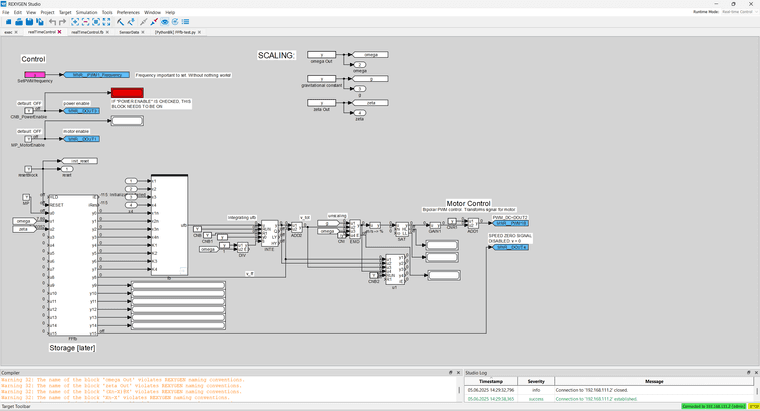
I am not sure how to make the stop in the lower right hand corner run