Complier issue
-
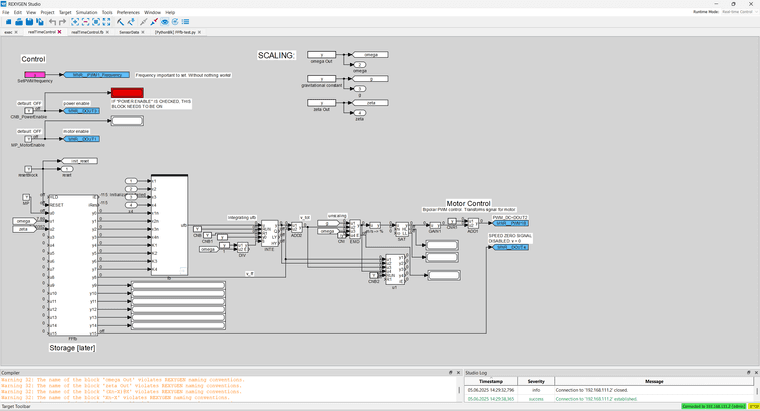
I am not sure how to make the stop in the lower right hand corner run
-
 C cechurat moved this topic from Communication (RS232, RS485, I2C, SPI, UDP, TCP, ...) on
C cechurat moved this topic from Communication (RS232, RS485, I2C, SPI, UDP, TCP, ...) on
-
Hi har,
thanks for your question. Please, can you share System Log? There should be some error which is preventing RexCore from running.
Cheers, Tomas
-
This post is deleted! -
@cechurat

I think the problem might be in the python block.import numpy as np
import time
from numpy import sin,cos,pi
from scipy.integrate import solve_ivp, solve_bvp, quad, odeint
from scipy.linalg import solve_continuous_are
from scipy.interpolate import interp1d
#import matplotlib.pyplot as plt
from PyRexExt import REXdef init():
global ω,ζ,π,τ,τ1,τpred,xmax,umax,θinti,θdotinit,xinit,xdotinit,xstate_init,θend1,θend2,θdotend,xend,xdotend,xstate_end1,xstate_end2,Q,R,ts,dt,ts1,bvpfcn,bcfcn,ff,uff0,uff,runningCost,A,B,mRiccati,Sall,Ball,Kall,fpred,us,j
global xstate_end,FFsol,X,uff,vs,Kvec,Xlast,Klast############################################ Define parameters ω = REX.u1.v ζ = REX.u2.v; # pendulum friction (scaled: 1 = critical damping) π = pi; # π = 3.14159... τ = 2*π # swingup time = 1 period, in scaled units τpred = 1 # allow for calculation time, in scaled units τ1 = 2*τ # for sim: swingup + balance time xmax = 2; # track limits at ±xmax umax = 5; # clip u for simulation test ONLY (not design) θinit = 0; # initial angle of pendulum θdotinit = 0.0; # initial angular velocity of pendulum xinit = 0.0; # initial position of cart xdotinit = 0.0; # initial velocity of cart xstate_init = np.array([θinit,θdotinit,xinit,xdotinit]) # eventually, from expt. θend1 = π # CCW swingup, assume θinit ∊ (-π,π) θend2 = -π # CW swingup θdotend = 0.0; # final angular velocity of pendulum xend = 0.0 * xmax; # final cart position xdotend = 0.0; # final cart velocity xstate_end1 = np.array([θend1,θdotend,xend,xdotend]) # modify for swing down, transport, ... xstate_end2 = np.array([θend2,θdotend,xend,xdotend]) # modify for swing down, transport, ... Q = np.diag([1,10,1,1]) # weighting for states for LQR R = np.array([10]) # weighting for input for LQR ts = np.arange(0, τ, 0.01*ω) # swing up in τ dt = 0.01*ω ts1 = np.arange(0, τ1, 0.01*ω) # swing up in τ, balance for another τ ############################################# Define functions def bvpfcn(t, X): # solve coupled state-adjoint system θ, θdot, x, xdot, λθ, λθdot, λx, λxdot = X dX = np.zeros((8, X.shape[1])) # array dimension is 8 * nx sinθ = sin(θ); cosθ = cos(θ) u = -λxdot + λθdot*cosθ dX[0] = θdot dX[1] = -sinθ - u*cosθ dX[2] = xdot dX[3] = u dX[4] = λθdot * (cosθ - u*sinθ) dX[5] = - λθ # dX[6] = -x**3 / xmax**4 # or: from running cost term (x/xmax)**4 dX[6] = 0 # running cost independent of x dX[7] = -λx return dX # Return derivatives (array) def bcfcn(x0, xτ): # boundary conditions for 4d-state at t = 0, τ dx0 = x0[0:4] - xstate_init # boundary condition for 4d state at t=0 dxτ = xτ[0:4] - xstate_end # bc at t=τ return np.hstack((dx0,dxτ)) # 8-dim vector for solve_bvp def ff(x0,xτ,τ): # ff state x0 → xτ in τ θinit,_,xinit,_ = x0 θend, _,xend, _ = xτ nt = 21 # number of time points, to start tvec = np.linspace(0, τ, nt) xλguess = np.zeros((8, nt)) # initial guesses for state trajectories xλguess[0, :] = np.linspace(θinit, θend, num=nt) # θ linear, θinit → θend xλguess[2, :] = np.linspace(xinit, xend, num=nt) # x linear, xinit → xend FFsol = solve_bvp(bvpfcn, bcfcn, tvec, xλguess, tol=0.1) # solve boundary-value problem return FFsol.sol def uff0(t): # feedforward acceleration (cannot evaluate on arrays) θ,_,_,_,_,λθdot,_,λxdot = FFsol(t) # evaluate interp funcs at time=t uff0 = -λxdot + λθdot*cos(θ) if t<τ else 0 return uff0 uff = np.vectorize(uff0) # define vectorized version (can call with array) def runningCost(t): # to calc cost of the feedforward command return 0.5*uff0(t)**2 def A(t): # dynamical matrix (local linear, nominal) θ = FFsol(t)[0] # FFsol from FF function Amat = np.zeros((4,4)) # 4 is from xstate.shape[0] Amat[0,1] = 1 Amat[1,0] = -cos(θ) + uff(t)*sin(θ) Amat[1,1] = 0 Amat[2,3] = 1 return Amat # evaluated at time t def B(t): # input vector (local linear, nominal) θ = FFsol(t)[0] # FFsol from FF function Bmat = np.zeros((4,1)) # 4 is from xstate.shape[0] Bmat[1] = -cos(θ) Bmat[3] = 1 return Bmat def mRiccati(t,S): # derivatives for matrix Riccati (vector form) Smat = S.reshape((4,4)) # convert 16 vector to 4x4 matrix A0 = A(t) # current dynamical matrix B0 = B(t) # current input vector dSmat = - A0.T @ Smat - Smat @ A0 - Q + Smat @ (B0 @ B0.T) @ Smat / R[0] dS = dSmat.reshape((16)) # convert 4x4 matrix to 16 vector return dS def Sall(Send,τ,tvec): # S matrix evaluated at times tvec Send1 = Send.reshape((16)) t_span = (τ, 0) # solve backwards in time, from τ → 0 Ssol1 = solve_ivp(mRiccati, t_span, Send1, dense_output=True).sol return Ssol1(tvec).reshape(4,4,tvec.size) # evaluate on tvec def Ball(FFsol,tvec): # input matrix (local linear, nominal) θ = FFsol(tvec)[0] nt = tvec.size Bmat = np.zeros((4,nt)) # 4 is from xstate.shape[0] Bmat[1] = -cos(θ) Bmat[3] = np.ones((nt)) return Bmat def Kall(Send,FFsol,τ,tvec): # for graphing tvec1 = np.clip(tvec, 0, τ) # elements beyond ff range are clipped to limits S = Sall(Send,τ,tvec1) # 4 x 4 x nt matrix (nt copies of 4x4 matrix B = Ball(FFsol,tvec1) # 4 x nt matrix (nt copies of 4-vector) return np.einsum('ijk,jk->ik', S, B)/R[0] # sum over inner index, element-mult tvec index def fpred(t,xstate): # dynamical eqs, for constant-v input θ, θdot, _, xdot = xstate # dynamical states dX = np.zeros((4)) # 4 is from xstate.shape[0] dX[0] = θdot dX[1] = -sin(θ) - 2*ζ*θdot # sim has pendulum friction, even if ff does not dX[2] = xdot dX[3] = 0 # driving term is vtot; utot is a derived variable return dX ############################################# prediction of future state xpred = solve_ivp(fpred, (0, τpred), xstate_init, dense_output=True).sol # predict future state xstate_init = xpred(τpred) # "initial" state, as predicted τpred in future θ0 = xstate_init[0]; # extrapolated θ0 might not be ∊ (-π,π) θ1 = (θ0+π) % (2*π) - π # modulus 2π xstate_init[0] = θ1 # new angle is ∊ (-π,π) ############################################# FF calculations xstate_end = xstate_end1; θend = θend1 FFsol = ff(xstate_init,xstate_end,τ) # ff solution for 4-state and 4-adjoint, 0→τ FFsol1 = FFsol Jff1 = 0.5*np.sum(uff(ts)**2)*dt # integrated running cost = overall cost xstate_end = xstate_end2; θend = θend2 FFsol = ff(xstate_init,xstate_end,τ) # ff solution for 4-state and 4-adjoint, 0→τ FFsol2 = FFsol Jff2 = 0.5*np.sum(uff(ts)**2)*dt # integrated running cost = overall cost REX.y11.v = f"feedforward cost: θend = π, Jff1 = {Jff1:0.2f}, θend = -π, Jff2 = {Jff2:0.2f}" if (Jff1 < Jff2): FFsol = FFsol1; xstate_end = xstate_end1 else: FFsol = FFsol2; xstate_end = xstate_end2 ############################################### fb calculations Aend = A(τ) # linear dynamics A matrix at t=τ Bend = B(τ) # linear input-coupling B vector at t=τ Send = solve_continuous_are(Aend,Bend,Q,R) # static S matrix from ARE Kvec = Kall(Send,FFsol,τ,ts1) # feedback gain vectors for t in ts1 ############################################### get arrays θs,θdot,x, xdot,_,_,_,_ = FFsol(ts) X = np.array([θs,θdot,x,xdot]) θlast,θdotlast,xlast,xdotlast,_,_,_,_=FFsol(2*π) # Evaluate last values Xlast = np.array([[θlast],[θdotlast],[xlast],[xdotlast]]) X = np.hstack((X,Xlast)) # add last value Klast = Kall(Send,FFsol,τ,2*π+0.1) Kvec = np.hstack((Kvec,Klast)) vs = np.hstack((xdot,0)) j=0def main():
start_test = time.perf_counter()
global j,X,uff,vs,Kvecif not REX.u0.v and j == 0: return else: REX.y15.v = True REX.y10.v= f"len(X)={len(X[0])}" if (j >= len(X[0])): REX.y8.v = 0 return # Value for every time REX.y0.v = X[0][j] REX.y1.v = X[1][j] REX.y2.v = X[2][j] REX.y3.v = X[3][j] REX.y4.v = Kvec[0][j] REX.y5.v = Kvec[1][j] REX.y6.v = Kvec[2][j] REX.y7.v = Kvec[3][j] REX.y8.v = vs[j] j += 1 test_time = time.perf_counter() - start_test REX.y9.v = f"test time = {test_time:0.3f} s" returndef exit():
# PUT YOUR CODE HERE
return -
@har Yes, the issue is in initialisation of the Python Block. If you wait a second with the mouse on the message

it will show you more instead of "..." which might help you to find the issue easier.Cheers,
Tomas -
@cechurat Hi Thomas when I hover my mouse over the error I get this message.

I am not quite sure what it means or how to fix it
-
@har Hi har,
Thanks for the additional info. We are not able to provide free support on this since it's your custom Python script. The error is not related to the Rexygen ecosystem. It seems that the CPU dispatcher is being initialised multiple times.
Tomas